Computing the genus of a punctured plane
In this example we will compute the genus of a punctured plane. In other words we are interested in the dimension of the 1st homology space.
First we need to create the mesh. Typically this is done in an external mesher such as gmsh but here we will construct it from scratch.
using CompScienceMeshes
h = 1/6
rect = meshrectangle(1.0, 1.0, h, 3)
hole = meshrectangle(1/3, 1/3, h, 3)
translate!(hole, point(1/3, 1/3, 0))
pred = overlap_gpredicate(hole)
all_faces = submesh((m,c)->!pred(chart(rect,c)), rect)Generating a structured mesh: The dimensions of the cuboid are
approximated by multiples of edge length. For exact dimensions and
unstructured grids, use kwarg - generator = :gmshNote that we started out creating a large rectangular mesh and a small one. Next we translate the small one to the center of the large one. We can use submesh to select the part of the mesh that does not coincide with the hole by providing an appropriate predicate.
The tricky bit is that in order to get the correct number, we need to discard any vertices and edges that lie on the boundary of the structure. To do this we first retrieve a list of all edges and vertices by again calling skeleton with the appropriate dimension. In a next step we select out those vertices and edges that are not on the boundary.
Note: overlap_predicate generates a predicate that takes cells of the same dimensionality as its argument. This means that we first need the 0-skeleton of the boundary before we can create a predicate that takes vertices of the original mesh.
all_edges = skeleton(all_faces, 1)
all_verts = skeleton(all_faces, 0)
bnd_edges = boundary(all_faces)
bnd_verts = skeleton(bnd_edges, 0)
#onbnd1 = overlap_gpredicate(bnd_edges)
#onbnd0 = overlap_gpredicate(bnd_verts)
interior_edges = submesh(!in(bnd_edges), all_edges)
interior_verts = submesh(!in(bnd_verts), all_verts)The set of interior_edges looks like this.
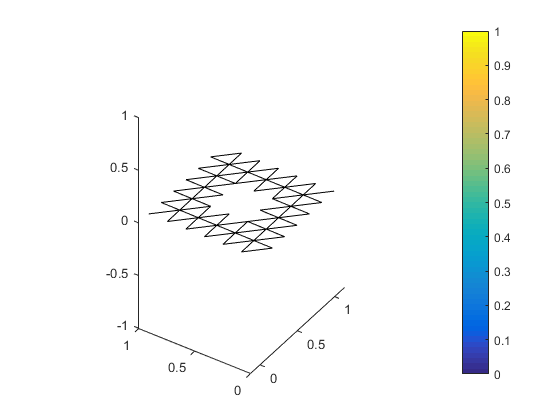
The co-boundary maps are simply the connectivity matrices between cells of the dimension 0-1 and 1-2, respectively. The genus can be computed by simply using the rank nullity theorem, but as part of this example we use the rank and nullspace on the connectivty matrices. This if desired can provide a representative of the cohomology space.
D0 = connectivity(interior_verts, interior_edges)
D1 = connectivity(interior_edges, all_faces)
using LinearAlgebra
nullity(A) = size(A,2) - rank(A')
genus = nullity(Matrix(D1)) - rank(Matrix(D0))1Of course we could have just computed Euler's number and deduced the genus from that:
1 - length(all_faces) + length(interior_edges) - length(interior_verts)1